《计算机组成与设计 硬件/软件接口》5.5 可信存储器层次（可用性、汉明编码）

Mar. 26, 2020

自从翻过了第四章之后就百无聊赖，主要是假期在某种意义上结束了，写了两个月的nodejs，今天开始陷入停滞，不如再水一篇~ 这是第五章将关于存储器层次结构的部分。5.7节的重点是汉明编码，我这才发现在数据校验上要花费相当多的代价来纠正一位错，检测两位错。

可信存储器层次

采用冗余技术构造可靠的存储器

5.5.1 失效的定义

首先是一些概念上的东西。

服务所处的两种可能的状态：

1. 服务实现：交付服务与需求相等
2. 服务中断：交付服务与需求不等

状态（1）到状态（2）的转换称为失效，状态（2）到状态（1）的转换称为恢复， 失效可以是永久性的，也可以是间歇性的。

可靠性、可用性

可靠性 是一个系统或模块能够持续提供用于需求的服务的度量，即从开始使用到失效的时间间隔

可靠性度量方法：平均故障时间（mean time to failure, MTTF)

年失效率（annual failure rate, AFR）在给定MTTF的情况下，在一年内预期器件的失效比例。

为了提高MTTF，可以提高器件的质量，也可以设计能够在器件失效的情况下继续工作的系统

1. 故障避免技术（fault avoidance）通过合理构建系统来避免故障的出现
2. 故障容忍技术（fault tolerance）采用荣誉措施，当发生故障时，通过荣誉措施保证系统仍能正常工作
3. 故障预报技术（fault forecasting）对故障进行预测，从而允许在器件失效前进行替换

5.5.2 纠正一位错，检测两位错的汉明编码(SEC/DED)

SEC/DED 指 Single Error Correcting, Double Error Detecting Code (SEC/DED) 汉明编码是由理查德·汉明（Richard Hamming）发明的一种广泛应用于存储器的冗余（redundant）技术 在汉明编码之前，仍然先从简单的地方开始。

二进制数距离

两个等长的二进制数的汉明距离是两个数对应位置不同的位的数量（通俗来讲，就是两个等长的二进制数的差别，对应位不同的数量），例如01010001和01110011有两位不同，所以他们的距离是2。 如果能够检测出一个码字是否有效，则可检测出一位的错误，称为1位错误检测编码。原书这里很绕，于是我找了下英文版的内容，以便理解

What happens if the minimum distance between members of a codes is two, and we get a one-bit error? It will turn a valid pattern in a code to an invalid one. Thus, if we can detect whether members of a code are valid or not, we can detect single bit errors, and can say we have a single bit error detection code。

算了，看不懂对后面倒也没什么影响。（“minimum distance between members of a codes"指的是最少两位的编码？然后里面有一位是错的，整个就是错的？）

用奇偶校验码进行错误检测：计算码字中的1的数量是奇数个还是偶数个，当一个字写入存储器时，奇偶校验位也被写入（1代表奇数，0代表偶数），也就是说，N+1位码字中1的个数永远为偶数，因此，当读出数据时，奇偶校验码也被读出并进行检测，如果计算出的校验码与保存的不符，则发生错误。

注意，奇偶校验码尽在有奇数个位出错时有效，而偶数个位出错是无法被检测到的。而且显然也不能进行纠错。

所以需要做的就是，让任意一个发生1位错的码字预期对应的合法码之间的距离要小于该非法码与其他合法码字的距离。以下便是**汉明纠错码（Hamming Error Correction Code, ECC）

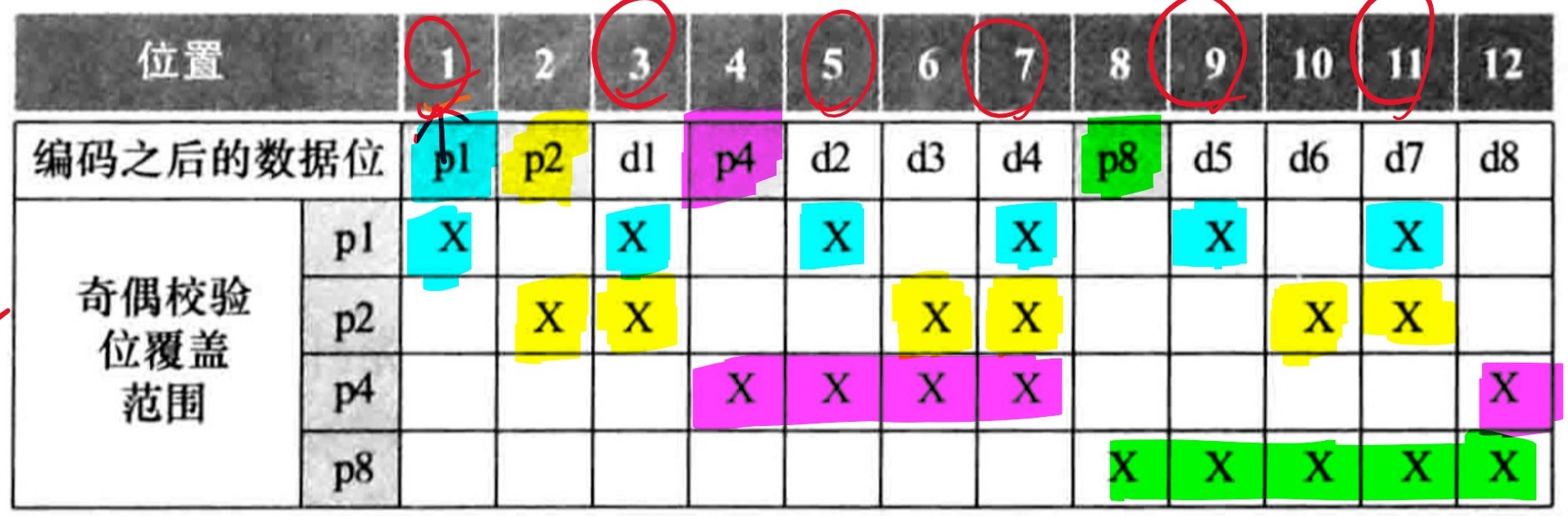
1. 对数据部分从左到右由1开始依次编号，这跟通常采用的从最右边开由0开始编号的做法相反。
2. 将所有编号为2的整数次幂的位标记为奇偶校验位（1，2，4，8，16……）。
3. 奇偶校验位的位置决定了其对应的数据位，如图。

• 校验位1（0001₂）检查第1，3，5，7，9，11……位，（这似乎是一个数字游戏）这些数位的编号的二进制形式最右边一位均为1（0001₂，0011₂，0101₂……）

• 校验位2（0010₂）检查第2，3，6，7，11，14，15……位，这些数位的编号的二进制形式右边起第二位均为1

• ……我在图中用不同的颜色标注，颜色对应检查的数据位

注意到每个数据位都被至少两个奇偶校验位覆盖，也就是说校验位组成的二进制数（XXXX₂），可以索引到每一个数据位，当数据出错时（1位错），只需要查看校验位组成的二进制数，即可定位到错误位置，然后修正（取反）。

我们现在已经有了1位纠错码，可以纠正1位的错误，如果在此基础上增加一位奇偶校验码（对整个字进行计算校验），就可以纠正1位错并检测两位错。

1	2	3	4	5	6	7	8
p1	p2	d1	p3	d2	d3	d4	p4

用H代替汉明奇偶校验位（p₁，p₂，p₃）

1. H为偶并且p₄为偶，表示没有错误发生。
2. H为奇并且p₄为奇，说明出现了1位可纠正错误。
3. H为偶并且p₄为奇，说明出错的仅仅是p₄，将p₄取反。
4. H为奇并且p₄为偶，这表示出现了两位错。