3.5 浮点运算

Jan. 30, 2020

有关计算机中浮点运算的部分，涉及IEEE 754标准 博客的公式差点挂了……

在计算机中，使用科学计数法表示二进制数

1.0_{2（底数F）} \times2^{-1（指数E）}

规格化二进制数

即小数点左边只有一位的使用科学计数法表示的实数，如 1.23 \times 10^{-2} 这样就不是规格化的二进制数： 12.3 \times 10^{-3} 在计算机中，浮点数以规格化二进制数表示

3.5.1 浮点表示

一般浮点数的表示

(-1)^s \times F \times 2^E$$

表示范围： $$2.0{10}\times 10^{-38} \sim2.0{10}\times 10^{38} $$

关于浮点数的溢出：

• 上溢（overflow） 指数太大而不能在指数域内表示
• 下溢（underflow）副指数太大而不能在指数域中表示

单精度与双精度

• 单精度（single precision）浮点数由一个32位字表示

• 双精度（double precision）浮点数由两个32位字表示

  双精度字占用两个32位字，由 符号位s 11位指数域， 52位尾数域构成

  可表示 $$2.0{10}\times 10^{-308} \sim2.0{10}\times 10^{308} $$

IEEE 754浮点标准

IEEE 754浮点标准是通用标准，通用语1980年后的每台计算机

隐藏了规格化二进制数的前导位1

因为在规格化数中，前导位肯定是非0位，而在二进制数中，非零位只有1，也就是说前导位必为1，所以完全可以隐藏掉

这样，可以为表示范围腾出更多空间

所以，单精度下，数有24（1+23）位宽

双精度下，数有53（1+53）位宽 $$(-1)^s \times (1+F)\times 2^E$$ 向十进制转换： $$(-1)^s \times [1+(s_1\times 2^{-1})+(s_2\times 2^{2})+(s_3\times 2^{-3})+(s_4\times 2^{-4})+\cdots]\times 2^E$$

IEEE 754浮点数标准还定义了一些其他的数学表述，比如$\pm \infin$，$\rm NaN$

$\rm NaN$ （Not A Number）可用于表示无效操作，可表示数学上的“不存在”（我不确定），用于让 程序员推迟程序中的一些测试和决定

使用符号位和数值的形式表示（而不是补码），便于快速进行整数比较

IEEE 754 带偏阶(biased notation)的计数法

目的

• 最小的负指数表示为 $000\cdots0000_2$
• 最大的正指数表示为 $111\cdots1111_2$

若采用补码形式，负指数看起来似乎是一个大得多的数

简而言之，偏阶就是给指数加上另一个数（偏阶），使他成为易于比较的（无符号）正整数

单精度的指数偏阶是127，

• 如指数为-1，则指数位为 $-1 + 127_10 = 126_10 = 0111\ 1110_2$

双精度的指数偏阶是1023，

综上所述，单精度的IEEE 754完整表示是 $$(-1)^s \times (1 + \rm Fraction)\times 2^{（Exponent - Bias)}$$

• Fraction 尾数
• Exponent 指数
• Bias 偏阶

例：使用浮点表示 $-0.75{10}$ $$-0.75{10} = -\frac{3}{4{10}} = -\frac{3}{2^2{10}}\\,\二进制小数形式：\qquad -\frac{11_2}{2_2^{10}} 或 -0.11_2\\,\科学计数法：\qquad-0.11\times2^0\\,\规格化计数：\qquad -1.12\times2^{-1}\\,\$$ 所以，$-0.75{10}$得单精度二进制格式为：

3.5.2 浮点加法

在浮点数计算中，浮点加法比浮点乘法复杂，因为存储的是规格化数，需要对齐小数点，而乘法不用对齐。

浮点加法，简单来说分为以下4步

1. 将有较小指数的数向较大指数对齐
2. 将有效数相加
3. 将结果调整为规格化科学计数的形式（同的检查指数上溢和下溢）
4. 根据精度要求进行舍入，若舍入后为非规格化科学计数形式，则返回3.

以下是在原书给出得算术单元结构上做的笔记：

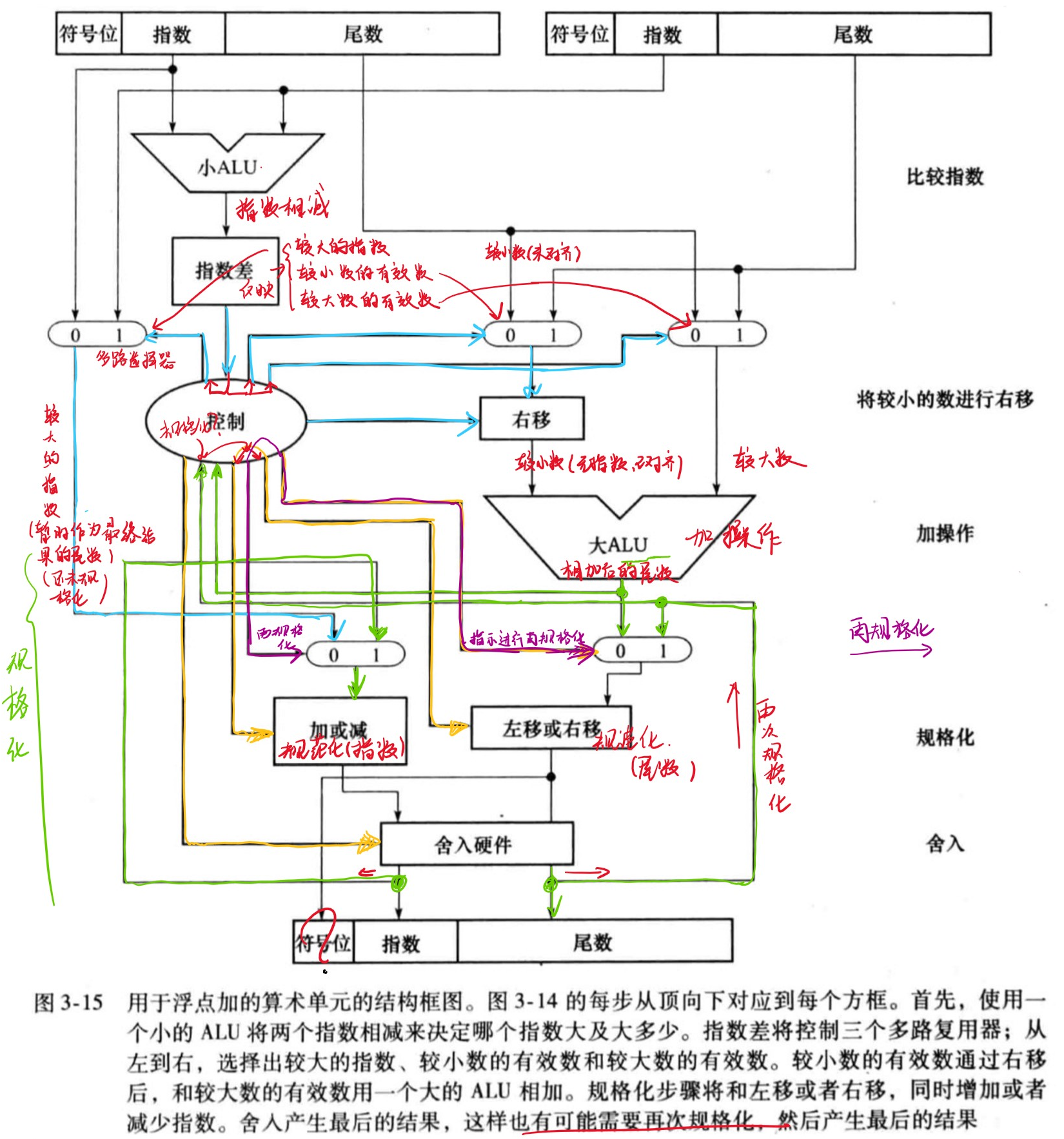
3.5.3 浮点乘法

浮点乘法相对直观

1. 处理带偏阶的指数 $$s = (s_1 - 127) + (s_2 -127) + 127 = s_1 + s_2 - 127$$
2. 计算有效数的乘法
3. 规格化积
4. 舍入
5. 得符号，同号为正，异号为负

3.5.4 MIPS中的浮点指令

可以参见资料，不再赘述

3.5.5 算术精确性

IEEE 754标准中规定了确保算术精确性的方法： 在计算过程中在右侧增加保护位和舍入位

• 保护位：在浮点数的中间计算中，在右边多保留的两位中的首位，用于提高舍入精度
• 舍入位：在浮点数的中间计算中，在右边多保留的两位中的第二位， 使浮点中间结果曼珠浮点格式，得到最接近的数

这是书中的一个例子，不方便打出来，就直接贴图了：

结果可以看到，采用保护位得到的结果是2.37，不采用保护位得到的结果是2.36，实际结果更接近前者。这说明了保护位的作用。可以联系一下我们做数学题的时候按要求四舍五入，总要往后算两位。

衡量浮点的精确性通常用尾数最低位(ulp)上有多少位的误差来衡量

IEEE 754 保证了计算机使用的数在半个ulp以内.

IEEE 754的舍入模式

• 向上舍入（向$+\infin$）
• 向下舍入（向$-\infin$）
• 截断舍入
• 向最近的偶数舍入

对于 0.5的情况，IEEE 754的做法是：如果最后一位是奇数，就+1；如果是偶数，就截去。

粘贴位

舍入位左边的数非零时置1，可让计算机区分 $0.50\cdots000{10}$和$0.50\cdots001{10}$

3.5.6 小结

IEEE 754标准浮点表示 $$ (-1)^s \times (1 + \rm Fraction)\times 2^{（Exponent - Bias)} $$